| CRYPTO. -+- par Sabrina | COUNTERSTRIKE - 3 |
| DATA ENCRYPTION SYSTEM (DES) |
I-
PRESENTATION
II-
DESCRIPTION
III- ETUDE D’UNE RONDE
VI- SECURITE DU DES
1- TABLE-S
2- METHODES D’ATTAQUE DU DES
ATTAQUE EXAUSTIVE
CRYPTANALYSE
DIFFERENTIELLE
D’AUTRES
TYPES DE CRYPTANALYSE
VII- LE DES ET SES DERIVES
TRIPLE-DES
DES UNIX
S-DES
VIII- CONCLUSION SUR LE DES
![]()
I- PRESENTATION
Le DES est un cryptosystème à clé privé: la même clé sert à la fois pour crypter et décrypter un texte. Créé en 1975 (?) et rendu public en 1976, le DES a longtemps et reste un des moyens les plus sûr pour crypter les données. A l'origine le DES fut développé par IBM pour répondre à de nouvelles exigences en matière de sécurité. Mais la NSA (National Security Agency) a repris les plans d'IBM pour améliorer (soit disant) les tables de permutations. De nombreuses polémiques sont nées d'une tel pratique mais aucune accusation réellement justifier n'à été trouvé contre la NSA (celle qui porte a croire que la NSA ont placé une "brèche secrète" dans les tables de permutations…).
Le DES (plus précisément le Triple-DES) est encore actuellement beaucoup utilisé car il maintient un niveau de sécurité tout à fait exceptionnel malgré son âge (25 ans). Si votre ennemi ne disposent pas de grand moyen soyez sûr que le DES gardera vos données confidentielles.
II- DESCRIPTION
La taille de la clé privé est de 56 bits et le bloc de donnée à crypter est de 64 bits. Pour des raisons informatiques usuelles, on code ces 56 bits dans 64 bits pour vérifier qu'il n'y a pas d'erreur dans la clé (contrôle par code correcteur d'erreur). Le DES est basé sur le principe très classique des rondes (16 rondes en tout). Pour schématiser une ronde, on peut dire qu'elle constitue une maille élémentaire à partir de laquelle la clé et le texte sont modifiés (l'une permuté, l'autre crypté un peu plus).
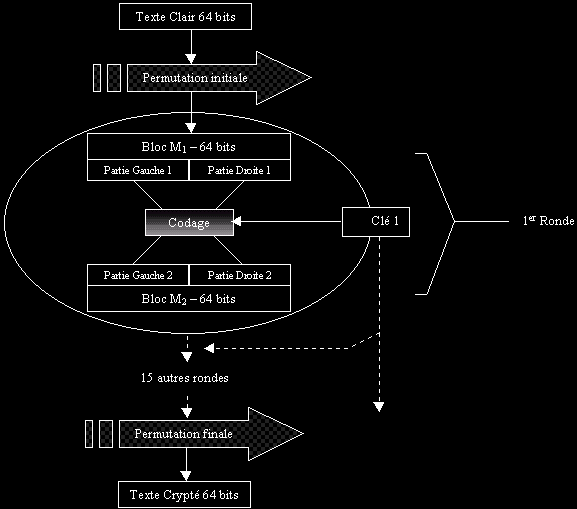
PLAN DU DES
Une ronde change le bloc à crypter et la clé. Chaque ronde à sa propre clé dérivée de la précédente. Le DES crypte sur un bloc de 64 Bits qu'il sépare en une partie droite et une partie gauche.
On a 16 rondes: chaque ronde dépendant donc d'une nouvelle clé et de nouveaux paramètres. On remarque que le bloc de 64 bits initial subit une permutation initiale (on mélange les bits) ; de manière analogue avant de posséder le bloc crypté, on effectue une permutation finale. (Parfois pour des raisons d’implémentation logicielle, on retire ces deux permutations ; un tel cryptage ne peut s’appeler DES mais reste tout aussi sûr)
Permutation Initiale
(58, 50, 42, 34, 26, 18, 10, 2, 60, 52, 44, 36, 28, 20, 12, 4, 62, 54, 46, 38, 30, 22, 14, 6, 64, 56, 48, 40, 32, 24, 16, 8, 57, 49, 41, 33, 25, 17, 9, 1, 59, 51, 43, 35, 27, 19, 11, 3, 61, 53, 45, 37, 29, 21, 13, 5, 63, 55, 47, 39, 31, 23, 15, 7)
REM : On notera les permutations comme des cycles. Par exemple, le bit 1 est remplacé par le bit 58, le 2nd par le bit 50 etc…
Permutation Finale
(40, 8, 48, 16, 56, 24, 64, 32, 39, 7, 47, 15, 55, 23, 63, 31, 38, 6, 46, 14, 54, 22, 62, 30, 37, 5, 45, 13, 53, 21, 61, 29, 36, 4, 44, 12, 52, 20, 60, 28, 35, 3, 43, 11, 51, 19, 59, 27, 34, 2, 42, 10, 50, 18, 58, 26, 33, 1, 41, 9, 49, 17, 57, 25)
III- ETUDE D’UNE RONDE
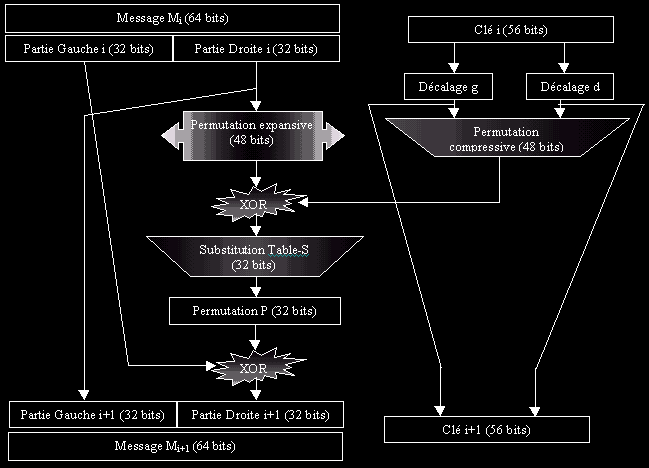
PLAN D'UNE RONDE
A chaque ronde, le message Mi est crypté à l’aide d’une nouvelle clé, issue d’une permutation de la clé précedente. Ces permutations (décalage g et décalage d) permettent donc de coder chaque ronde avec une clé différente ; ces permutations gauche et droite de la clé s’exercent sur 28 bits de la clé (on retrouve bien 56 = 28 +28 ). Voici résumé la table des décalages de la clé :
Décalage des Clés
|
Numéro
de ronde
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
|
Décalage
|
1
|
1
|
2
|
2
|
2
|
2
|
2
|
2
|
1
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
Ainsi à la ronde 4, la clé est décalé de 2 bits vers la gauche.
Le message Mi est séparé en deux parties : une droite et une gauche. La partie droite représentera la partie Gauche du message Mi+1. Pour former la partie Droite du message Mi+1, on gonfle la partie Droite de Mi en un bloc de 48 bits (permutation expansive). Ce bloc est codé par un XOR avec la clé correspondant au numéro de la ronde. Ce nouveau bloc (que l’on peut dire crypté) subit une compression par table-S afin qu’il retrouve une taille de 32 bits. Les tables-S sont un points cruciales dans la cryptographie DES. Ensuite, ce bloc subit tour à tour une Permutation-P et un XOR avec la partie Gauche du message Mi. On obtient ainsi le nouveau message Mi+1 avec parallèlement la nouvelle Clé pour la futur ronde.
Reste donc à présenter les différents tableaux :
Permutation Compressive de la Clé
(14, 17, 11, 24, 1, 5, 3, 28, 15, 6, 21, 10, 23, 19, 12, 4, 26, 8, 16, 7, 27, 20, 13, 2, 41, 52, 31, 37, 47, 55, 30, 40, 51, 45, 33, 48, 44, 49, 39, 56, 34, 53, 46, 42, 50, 36, 29, 32)
Permutation Expansive de la partie Droite de Mi
(32, 1, 2, 3, 4, 5, 4, 5, 6, 7, 8, 9, 8, 9, 10, 11, 12, 13, 12, 13, 14, 15, 16, 17, 16, 17, 18, 19, 20, 21, 20, 21, 22, 23, 24, 25, 24, 25, 26, 27, 28, 29, 30, 31, 32, 1)
REM: Ici, le bloc d’entrée et le bloc de sortie n’ont pas la même taille. On prendra donc garde de lire : le premier bit du bloc de sortie vaut le bit 32 du bloc d’entrée ; de même le 4eme bits du bloc de sortie vaut le 3eme bit du bloc d’entrée etc.
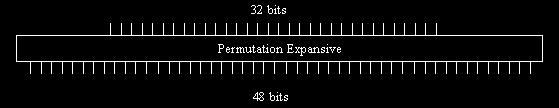
Voyons maintenant les tables-S. Ces tables donnent donc conformément au schéma d’une ronde : 48 bits en entrée et renvoie 32 bits en sortie. Elle effectues donc une sorte de compression. Bien sûr, ce n’est pas une véritable compression au sens de la théorie de l’information car il ne faut pas perdre de vue que la Permutation Expansive à gonfler notre message.

On prend notre bloc de 48 bits par paquets de 6 bits. Et on applique la table-S pour obtenir en sortie 4 bits. Pour lire les 48 bits d’entrée, il faut donc 8 table-S (6*8=48). Chacune de ces tables-S sont différentes. On représente usuellement ces tables-S par des matrices 4*16.
Table-S 1
|
14
|
4
|
13
|
1
|
2
|
15
|
11
|
8
|
3
|
10
|
6
|
12
|
5
|
9
|
0
|
7
|
|
0
|
15
|
7
|
4
|
14
|
2
|
13
|
1
|
10
|
6
|
12
|
11
|
9
|
5
|
3
|
8
|
|
4
|
1
|
14
|
8
|
13
|
6
|
2
|
11
|
15
|
12
|
9
|
7
|
3
|
10
|
5
|
0
|
|
15
|
12
|
8
|
2
|
4
|
9
|
1
|
7
|
5
|
11
|
3
|
14
|
10
|
0
|
6
|
13
|
Table-S 2
|
15
|
1
|
8
|
14
|
6
|
11
|
3
|
4
|
9
|
7
|
2
|
13
|
12
|
0
|
5
|
10
|
|
3
|
13
|
4
|
7
|
15
|
2
|
8
|
14
|
12
|
0
|
1
|
10
|
6
|
9
|
11
|
5
|
|
0
|
14
|
7
|
11
|
10
|
4
|
13
|
1
|
5
|
8
|
12
|
6
|
9
|
3
|
2
|
15
|
|
13
|
8
|
10
|
1
|
3
|
15
|
4
|
2
|
11
|
6
|
7
|
12
|
0
|
5
|
14
|
9
|
Table-S 3
|
10
|
0
|
9
|
14
|
6
|
3
|
15
|
5
|
1
|
13
|
12
|
7
|
11
|
4
|
2
|
8
|
|
13
|
7
|
0
|
9
|
3
|
4
|
5
|
10
|
2
|
8
|
5
|
14
|
12
|
11
|
15
|
1
|
|
13
|
6
|
4
|
9
|
8
|
15
|
3
|
0
|
11
|
1
|
2
|
12
|
5
|
10
|
14
|
7
|
|
1
|
10
|
13
|
0
|
6
|
9
|
8
|
7
|
4
|
15
|
14
|
3
|
11
|
5
|
2
|
12
|
Table-S 4
|
7
|
12
|
14
|
3
|
0
|
6
|
9
|
10
|
1
|
2
|
8
|
5
|
11
|
12
|
4
|
15
|
|
13
|
8
|
11
|
5
|
6
|
15
|
0
|
3
|
4
|
7
|
2
|
12
|
1
|
10
|
14
|
9
|
|
10
|
6
|
9
|
0
|
12
|
11
|
7
|
13
|
15
|
1
|
3
|
14
|
5
|
2
|
8
|
4
|
|
3
|
15
|
0
|
6
|
10
|
1
|
13
|
8
|
9
|
4
|
5
|
11
|
12
|
7
|
2
|
14
|
Table-S 5
|
2
|
12
|
4
|
1
|
7
|
10
|
11
|
6
|
8
|
5
|
3
|
15
|
13
|
0
|
14
|
9
|
|
14
|
11
|
2
|
12
|
4
|
7
|
13
|
1
|
5
|
0
|
15
|
10
|
3
|
9
|
8
|
6
|
|
4
|
2
|
1
|
11
|
10
|
13
|
7
|
8
|
15
|
9
|
12
|
5
|
6
|
3
|
0
|
14
|
|
11
|
8
|
12
|
7
|
1
|
14
|
2
|
13
|
6
|
15
|
0
|
9
|
10
|
4
|
5
|
3
|
Table-S 6
|
12
|
1
|
10
|
15
|
9
|
2
|
6
|
8
|
0
|
13
|
3
|
4
|
14
|
7
|
5
|
11
|
|
10
|
15
|
4
|
2
|
7
|
12
|
9
|
5
|
6
|
1
|
13
|
14
|
0
|
11
|
3
|
8
|
|
9
|
14
|
15
|
5
|
2
|
8
|
12
|
3
|
7
|
0
|
4
|
10
|
1
|
13
|
11
|
6
|
|
4
|
3
|
2
|
12
|
9
|
5
|
15
|
10
|
11
|
14
|
1
|
7
|
6
|
0
|
8
|
13
|
Table-S 7
|
4
|
11
|
2
|
14
|
15
|
0
|
8
|
13
|
3
|
12
|
9
|
7
|
5
|
10
|
6
|
1
|
|
13
|
0
|
11
|
7
|
4
|
9
|
1
|
10
|
14
|
3
|
5
|
12
|
2
|
15
|
8
|
6
|
|
1
|
4
|
11
|
13
|
12
|
3
|
7
|
14
|
10
|
15
|
6
|
8
|
0
|
5
|
9
|
2
|
|
6
|
11
|
13
|
8
|
1
|
4
|
10
|
7
|
9
|
5
|
0
|
15
|
14
|
2
|
3
|
12
|
Table-S 8
|
13
|
2
|
8
|
4
|
6
|
15
|
11
|
1
|
10
|
9
|
3
|
14
|
5
|
0
|
12
|
7
|
|
1
|
15
|
13
|
8
|
10
|
3
|
7
|
4
|
12
|
5
|
6
|
11
|
0
|
14
|
9
|
2
|
|
7
|
11
|
4
|
1
|
9
|
12
|
14
|
2
|
0
|
6
|
10
|
13
|
15
|
3
|
5
|
8
|
|
2
|
1
|
14
|
7
|
4
|
10
|
8
|
13
|
15
|
12
|
9
|
0
|
3
|
5
|
6
|
11
|
La lecture d’une table-S est très particulière (ce qui permet de conférer la sécurité du DES – la non linéarité du DES – nous en reparlerons plus tard). Rappelons donc que l’on reçoit 6 bits en entrée ; bits que l’on note b1b2b3b4b5b6. On forme le nombre b1b6 (2 bits) qui correspond donc à une valeur décimale comprise entre 0 et 3. Cette valeur représentera la ligne de lecture. De manière analogue, b2b3b4b5 représente un nombre décimal compris entre 0 et 15. Cette valeur représentera la colonne de lecture.
Donnons un exemple :
Nous sommes à la table-S 5 (en d’autres termes les bits compris entre 25 et 30). Les bits retenus sont 110011. (b1=1 b2=1 b3=0 b4=0 b5=1 b6=1). Le premier bit et le dernier (b1 et b6) forment 11 (=b1b6) qui représente la valeur décimale 3. Puis, les bits b2b3b4b5 valent 1001 représentant en décimal la valeur 9. Ainsi dans la table-S 5, on lira le nombre à la ligne 3 et à la colonne 9 ; c’est-à-dire le nombre 15. Attention, les lignes et colonnes sont numérotés à partir de 0 !
La substitution par table-S remplace donc le bit 25-30 : 110011 par 111111 (15 en décimal). Le caractère assez particulier de l’utilisation des tables-S prendra tout son intérêt par la suite.
Comme l’indique le schéma général d’une ronde, il reste une dernière permutation. Permutation-P de 32 bits. Cette permutation précède un XOR avec la partie gauche Mi.
Permutation-P
(16, 7, 20, 21, 29, 12, 28, 17, 1, 15, 23, 26, 5, 18, 31, 10, 2, 8, 24, 14, 32, 27, 3, 9, 19, 13, 30, 6, 22, 11, 4, 25)
IV- DECRYPTAGE DU DES
Les instructions de cryptage du DES ne sont pas innocentes. L’un des atouts majeurs du DES est la facilité du décryptage. En effet, l’algorithme de décryptage est le même que pour le cryptage. Cela peut sembler surprenant à priori mais le DES a était conçu pour être involutif, un peu (dans une complexité moindre) comme le XOR.
Toutefois, il faut garder quelques précautions avant d’appliquer formellement le déchiffrement. Ainsi, les clés doivent être générées dans l’ordre inverse. Par exemple, si on note Ci la clé qui sert à chiffrer la ième ronde, au cryptage on utilisera donc C1, C2, …., C16 mais on utilisera C16, …, C1 au déchiffrement. De manière analogue, les décalages des clés deviennent inverse de l’ordre de chiffrement pour donner :
Décalage des Clés
| Numéro de ronde | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| Décalage | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 1 |
V- MODE PROPRE DU DES
Comme tout cryptosystème, le DES utilise différent mode de codage. Ces méthodes sont tout à fait générale et nous profitons de la présentation du DES pour les exposer.
Mode ECB (Electronic CodeBook)
Certainement considéré comme le plus intuitif de tous, le mode ECB consiste à crypter un bloc de taille fixe (64 bits pour le DES) avec toujours la même clé C. On sépare (virtuellement) le fichier à crypter en bloc de 64 bits et on applique le DES sur chacun de ces blocs avec la clé C.
Le principal défaut d’une telle méthode consiste dans la redondance du code utilisé ; si on connaît en clair et crypté un bloc de 64 bits, dès que l’on retrouvera le même bloc crypté on pourra retrouver instantanément le bloc clair correspondant. On pourra donc construire une table de " correspondance inverse " permettant de remonter, à partir d’échantillon, le texte crypté.
Mode CBC (Cipher Block Chaining)
Cette méthode comble les défauts du mode ECB en réutilisant le bloc précédemment crypté. Ainsi, un bloc Mi codé avec la clé C en Wi sera utilisé pour le codage de Mi+1 : on effectue un XOR entre Wi et Mi+1 pour obtenir Wi+1 (avec la même clé C). On utilise un mécanisme dit de " rétroaction ".
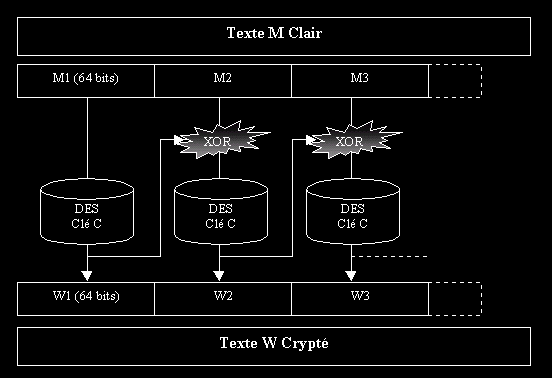
On effectue donc un calcul de proche en proche des blocs cryptés. Pour décrypter un message, on commencera par déchiffrer le premier bloc pour le combiner avec un XOR au second bloc déchiffrer.
Il existe d’autres modes propres du DES (et d’un cryptosystème en général) mais ils sont plutôt utilisés pour l’authentification et sortent du cadre de cet article. Le mode ECB est d’ailleurs le seul réellement utilisé par les logiciels. Si vous désirez un complément d’information sur les autres modes propres envoyez-moi un mail.
VI- SECURITE DU DES
1- TABLE-S
Dans tout le processus de cryptage du DES, il faut savoir que seul les tables-S assurent la sécurité du DES (disons au moins d’un point de vu théorique). En effet, les tables-S ont la particularité d’empêcher / amoindrir les méthodes de cryptanalyse. Celles-ci confinent les informations du message initial : on passe en effet de 48 à 32 bits. L’information est en quelques sorte diffusé: ce qui permet d’augmenté la difficulté d’analyse d’une attaque consistant à comparer les différences entre 2 textes chiffrés avec la même clé (une telle méthode s’appelle cryptanalyse différentielle). Bien sûr, ces tables-S n’ont pas étaient conçu n’importe comment ; de nombreux critères on consistée à rendre la distribution le plus aléatoire possible (on ne doit pas pouvoir déduire certains bits par l’addition ou le XOR d’autres bits). Malheureusement, quand je vais vous dire que ces tables-S ont été conçues par la NSA, vous allez immédiatement douter (à juste titre :) au caractère aléatoire de ces tables. Ces tables-S ont en effet étaient conçu par l’espion international ; de nombreux cryptologue et mathématiciens se sont penchés sur une éventuelle " Brèche secrète " (qui permettrait de casser facilement le DES). Toutefois, la NSA ne semble pas avoir introduit de telle brèche, qui plus est ces tables-S ne sont pas plus curieuses que d’autres. Cette polémique est maintenant bien éteinte (surtout depuis l’arrivé du AES – Advanced Ecryption System).
2- METHODES D’ATTAQUE DU DES
ATTAQUE EXAUSTIVE
Le but de l’attaque est d’essayer toutes les clés possibles (2^56). Pour cela on suppose que l’on dispose du texte crypté et clair. On chiffre le texte clair à l’aide de la clé supposé puis on le compare au texte crypté ; s’il corresponde alors on a trouvé la bonne clé (disons avec une probabilité certaine) : dans la pratique 64 bits de texte suffisent.
Bien sûr, tout comme le Xor (cf. Article : Cryptosystème XOR) cette méthode nécessite beaucoup de ressource CPU et de temps. Mais avec le matériel actuel, ce n’est plus aussi impossible qu’il y a quelques années ; d’ailleurs certaines machines n’ont été construite dans ce seul but (ces messieurs de la NSA savent de quoi je parle).
Reste à émettre certain doute d’une telle méthode pour des clés plus importantes. Pour des clés de 128bits utilisant le DES (voir plus loin le Triple-DES) une telle méthode n’est absolument pas employable (il faut compter plusieurs siècles sur une machine utilisant autant de silicium que notre terre en compte).
CRYPTANALYSE DIFFERENTIELLE
Cette méthode de cassage du DES est relativement récente (1990) est constitue la voie la plus prometteuse dans la cryptanalyse. On suppose détenir de nombreuse version de texte en clair et crypté (avec la même clé). Cette méthode consiste à étudier les différences entre le texte en clair et le texte chiffré à l’aide des différences qu’apportent les tables-S, les permutations, les XOR. Ceci permet d’émettre des critères, ces même critères permettant de converger vers la clé.
Nous verrons dans un prochain texte l’application de cette méthode ACTUELLEMENT utilisée pour décrypter le DES, mais également pour tout autre cryptosystème à clé privée.
D’AUTRES TYPES DE CRYPTANALYSE
Le cryptanalyse à clé corrélée. Elle consiste cette fois à s’appuyer sur l’action de différentes clés sur un texte clair, pour en étudier les différences avec le texte effectivement crypté. Elle nécessite trop de texte clair et crypté pour être raisonnablement utilisé.
La cryptanalyse dite cryptanalyse linéaire. Celle-ci est également très récente mais fait preuve d’une complexité terrifiante. Elle fera peut-être preuve d’une explication future.
VII- LE DES ET SES DERIVES
Le DES n’est plus utilisé de manière brute comme précédemment développé. On utilise souvent des variantes permettant d’utiliser des clés plus grandes ou/et un chiffrement plus sûr.
TRIPLE-DES
Le DES possède une propriété importante et qui n’est pas commune à tous les cryptosystèmes à clé privée. Le DES ne constitue pas un groupe, si vous crypté un texte par DES sur un texte T avec une clé C1, si vous chiffrez de nouveau avec une clé C2 (on parle de surchiffrage) alors ceci ne reviens pas a chiffré avec une clé C3. De la peut paraître une propriété bénigne, voir vrai à fortiori, mais cette propriété n’est pas vraie pour le XOR par exemple.
Ainsi, crypté 3 fois un texte avec une clé C1,C2,C3 augmente par 3 votre niveau de sécurité. Tel est le principe du Triple-DES, ceci permet d’utiliser des clés plus grandes.

DES UNIX
Crypt(3) utilise un algorithme comparable au DES mais avec de légère variante afin d'éviter (à l’époque) l’utilisation des puces spécialisées au cassage du DES.
S-DES
Ce DES utilise d’autres tables-S pour renforcer la sécurité mais tout comme les tables-S du DES original rien ne prouve leur validité.
Certaines versions du S-DES utilisent des tables-S dépendant de la clé. Ceci diminue fortement les chances de réussir une cryptanalyse différentielles. On retient d’ailleurs généralement cette solution avec le Triple-DES pour chiffrer les données.
VIII- CONCLUSION SUR LE DES
25 ans plus tard le DES est toujours là. Il constitue un moyen très sûr pour quiconque voudrait garder des données confidentielles. Mais il faut connaître vos ennemis. En effet, en 25 ans les travaux (secret généralement et rendu publique une fois de nouvelles méthodes plus performantes trouvées) sont considérables, si votre ennemis numéro 1 est la NSA alors passez votre chemin (d’une part car se sont eux qui ont conçu le DES et surtout car se sont eux qui possèdent les plus gros moyen au monde en matière de cryptanalyse) par contre si votre ennemi s’appelle Mr Dutieulle alors là il n’y a aucun risque. Soyez assuré qu’un triple-DES assure un niveau de confidentialité exceptionnel contre la plus part des utilisateurs.
Quel est l’avenir pour le DES ? Afin de sauver le droit d’expression, la liberté des idées et au nom de l’indépendances, les scientifiques ont mis en place (à l’heure où j’écris ces lignes 1er semestre 2000) un nouveau cryptosystème pour remplacer définitivement le DES : son nom est l’AES (Advanced Encryption System). Le principal atout du AES est la taille de la clé pouvant dépasser les 128 bits. Mais surtout la facon dont a été penser le AES. A l’époque du DES (1975), les informations au niveau cryptologie étaient classé secret-défense, maintenant libre à chacun de disposer des avancés actuelles (du moins celles rendues publique ou découverte par les grandes universités) ceci renforçant la sécurité des nouveaux algorithmes.
Pour connaître les dernières découvertes sur le DES (et de nombreux liens) : www.rsa.com
Pour toutes questions, commentaires, critiques, erreurs: sabrina@inorbit.com