Pour ce premier numéro, je vous propose un algorithme de cryptage matriciel 128 bits, que j'ai créé et codé.

Vous connaissez tous le nouvel algorithme cryptographique du standard américain, l’AES ou Rinjdael. Cet algorithme est matriciel, autrement dit il fonctionne avec des matrices de chiffres, et code n’importe quoi de cette manière. Je me suis donc attelé à la tâche, et j’ai conçu un algorithme de ce genre, plus simple mais pas forcément moins sécurisé.

Le principe est assez simple. La législation française (encore elle) nous limite à 128 bits en taille de clé. Afin de rendre cet algorithme légal, je suis donc obligé de la respecter. En terme de matrice, sachant que je ne vais manipuler que des entiers, je retiens comme clé une matrice de 4 octets sur 4, soit 16 cases de 8 bits (les entiers sont en fait des caractères) ce qui donne bien 128 bits de clé. Ce qui implique logiquement un cryptage par bloc de 128 bits, ce qui n’est pas désagréable à réaliser.

Mais voyons donc l’algorithme, car c’est celui-ci qui est le cœur même du codage.

Un utilisateur lambda, (on va l’appeler John ;) se crée une clé aléatoire, ou pseudo-aléatoire, de 128 bits, qui lui servira pour encoder.

John veut donc crypter un message M de taille n (en octets). Si n n’est pas un multiple de 16, le dernier bloc ne sera pas complet. Il faut donc palier à cet inconvénient, en jouant sur la structure du crypté.

On peut donc déjà définir qu’il faudra un caractère qui indiquera le nombre d’octets (d’entiers) à ne pas prendre en considération une fois le message décrypté. Dans mon cas, je vais juste indiquer le nombre d’entiers à ne pas prendre en compte dans le dernier bloc.

On obtient une structure de ce type : 

L’extra est en fait un entier codé sur 8 bits (et donc un short int) qui indique le nombre d’entiers à ne pas prendre en compte dans la dernière matrice.

1)       Algorithme de cryptage

L’algorithme de cryptage en lui-même est assez complexe. Il est basé sur deux opérations simples et rapides à effectuer : le XOR (Ou Exclusif) et le modulo.

Chaque matrice claire subit, par tour, trois transformations :

-          Un XOR bit à bit avec la matrice clé

-          Un décalage des colonnes différent suivant la ligne (Row Shift)

-          Un décalage des lignes différent suivant la colonne (Col Shift)

On effectue n tours, statistiquement déterminé à 12, afin de rendre le cryptage solide.

Après chaque n tours, pour les blocs situés après le premier, on ajoute une clé de brouillage, dépendante du crypté précédent, qui permet d’éviter toute redondance. Cette clé de brouillage est en fait le crypté précédent, crypté avec 1 tour.

Pour le dernier bloc, les entiers manquants sont tirés aléatoirement, afin de rendre plus difficile la cryptanalyse .

Voici le schéma de cryptage :  

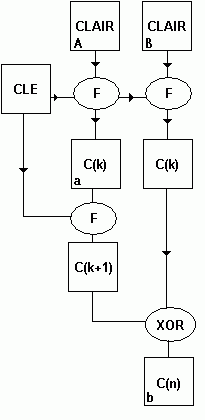
Ce schéma est un exemple pour un message de deux blocs, donc de 256 bits (soit 32 octets). Le premier bloc (A) subit une transformation par F (qui est en fait les trois transformations réunies) et on obtient C(k) avec k le nombre de tours effectués. Pour le bloc (B), on obtient premièrement C(k), puis C(n) car on fait un XOR bit à bit avec le bloc  C(k+1) précédent. On écrit dans le fichier le bloc (a), puis (b), puis les suivants. Le premier C(k) permettra de chaîner les C(k+1) afin de permettre le décryptage.

L’avantage de cette méthode est de constituer un flux. Si quelqu’un intercepte le flux, il ne possède pas C(k+1) et ne peux donc pas décrypter le message en cours de transmission. Cette clé de brouillage a été ajouté pour éviter la redondance cyclique (tous les 128 bits) et aussi afin d’empêcher l’interception de flux.

En ce qui concerne les clés, elles sont générées pseudo-aléatoirement, et cela donne un nombre de clés possibles de 3,1028 x 10³⁸. Beaucoup quoi !

2)       Calculs des décalages

Les décalages sont calculés à partir de la clé. En faisant un OU EXCLUSIF global de tous les entiers d’une ligne, on obtient un entier dh_i (avec i le numéro de la ligne) qui est en fait le décalage de cette ligne. Idem pour le décalage des colonnes. Afin que ce décalage soit possible, on calcule d=dh_i mod 4, ce qui permet d’effectuer une rotation cyclique de la rangée, comme ceci :

Si cette rangée subit un décalage de 3 on obtient alors :

3)       Algorithme de décryptage

Pour le décryptage , on applique le même principe mais avec F^-1 , c’est à dire que l’on effectue les transformations en sens inverse, et on peut décrypter ainsi un message codé de cette manière. Attention, il faut d’abord trouver le premier C(k+1) en cryptant le premier bloc du crypté (un seul tour) avec la clé. Ensuite on applique juste la procédure inverse.

Je vous fournis avec cet article les codes sources des procédures principales (commentés) disponible sur le serveur d’Espionet, mais l’algorithme principal n’est pas terminé. Sachez toutefois que ces sources sont fonctionnelles, et que vous disposez de toutes les fonctions nécessaires à l’algorithme.

Il va de soi que ce code source n’est que le résultat actuel de recherches en cours, et qu'il n’est donc pas optimisé, de manière à rendre aussi claire que possible la méthode employée. Ne vous étonnez pas si vous remarquez les mêmes structures ou le même code dans les différentes fonctions. Pour l’instant, ces fonctions renvoient juste une adresse d’un tableau de 16 entiers, afin de faciliter ensuite le travail. L’utilisation de pointeurs dans l’algorithme principal sera donc nécessaire.

4)       Conclusion

Cet algorithme a été testé, et marche correctement . Il est recommandé de choisir n entre 10 et 14 pour avoir une puissance de cryptage maximale. Utilisez ce code source à bon escient, il appartient à la communauté. J’espère que vous aurez compris le fonctionnement d’un cryptage matriciel, grâce à cet exemple.

e-mail: virtualabs@ifrance.com 

 Greetz to : @i.corps  and CoCo

-----------------------------------------------------------------------

Virtualabs  

Pour me contacter :

Virtualabs : virtualabs@ifrance.com